Tịnh tiến đồ thị song song với trục tọa độ
Định lý: Cho \(\left( G \right)\) là đồ thị của $y = f\left( x \right)$ và \(p > 0,\,\,q > 0\); ta có
Tịnh tiến \(\left( G \right)\) lên trên $q$ đơn vị thì được đồ thị $y = f\left( x \right) + q$
Tịnh tiến \(\left( G \right)\) xuống dưới $q$ đơn vị thì được đồ thị $y = f\left( x \right)-q$
Tịnh tiến \(\left( G \right)\) sang trái $p$ đơn vị thì được đồ thị $y = f\left( {x + p} \right)$
Tịnh tiến \(\left( G \right)\) sang phải $p$ đơn vị thì được đồ thị $y = f\left( {x-p} \right)$
Ví dụ:
Tịnh tiến đường thẳng $(d)$: $y=x-1$ sang phải 3 đơn vị thì được đồ thị của hàm số nào?
Giải:
Kí hiệu $f(x)=x-1$, theo định lý trên, khi tịnh tiến đồ thị hàm số $f(x)$ sang phải 3 đơn vị thì ta được đường thẳng $(d')$ có phương trình là $y=f(x-3)=(x-3)-1=x-4$
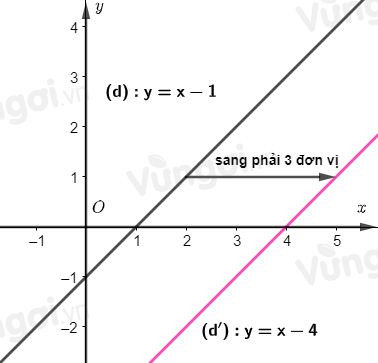
- Lý thuyết liên quan
Đại cương về hàm số --- Xem chi tiết tại đây.
Hàm số --- Xem chi tiết tại đây.
